Un bref aperçu de haskell

Les listes infinies sont une des nombreuses possibilités offertes par un langage paresseux. C'est souvent d'elles dont on entend le plus parler pour présenter le haskell, alors qu'il ne s'agit pourtant que d'une fonctionnalité original parmi tant d'autres. Cela est sûrement du au fait que la notion d'infinie éveille la curiosité des développeurs habitué à un monde impératif où les tableaux, les listes, et toute structure mémoire est finie. Bref, trêve de bavardages et de suppositions fumeuses.

De tels listes peuvent exister grâce au caractère paresseux de haskel : tant que vous n'avez pas besoin de la valeur situer à la xième position, alors toute la portion (infinie) de la liste qui lui succède ne sera ni évaluée, ni présente en mémoire, ni parcourue.

Comment faire de telles listes? Par récursion ou par compréhension. La façon la plus simple est la définition de liste par compréhension, c'est à dire une définition de la forme "L'ensemble des f(trucs) pour les quels P(truc) est vraie". Où f est une formule sur "trucs" et où P est une proposition, disons une fonction qui renvoie True ou False.

Commençons par des liste en compréhension finies :

-- "x <- l" signifie "pour x se baladant dans la liste l"
-- l1 = [1, 2, 3, 4, 5]
l1 = [x | x <- [1, 2, 3, 4, 5]]
-- L'opérateur c/c++ != s'écrit /=
-- l2 = [1, 2, 4, 5]
l2 = [x | x <- [1, 2, 3, 4, 5], x /= 3]

-- l3 = [2, 4, 8, 16, 32]
l2 = [2^x | x <- [1, 2, 3, 4, 5]]

-- l4 = [2, 4, 16, 32]
l4 = [2^x | x <- [1, 2, 3, 4, 5], x /= 3]

En fait, c'est une sorte de sucre syntaxique. Le soucis, c'est que ce que cache les listes en compréhension (monades) ne sera aborder que dans la troisième partie. On prendra donc notre mal en patience.

Pour en revenir a nos listes en compréhension infinie, on peut penser à "l'ensemble des entiers qui sont paire" ou. Voici quelques listes infinies :

--La liste de tous les entiers à partir de 42 peut s'écrire [42..]
liste_infinie_des_entiers = [1..]

--Pour calculer x % 2 (c/c++), on écrit "x `mod` 2", ou encore "mod x 2".
-- La fonction even :: Int -> Bool indique si un nombre est paire.

liste_des_entiers_paires   = [2 * x | x <- [1..]]
-- On peut rajouter des conditions séparé par des virgules
liste_des_entiers_paires'  = [x | x <- [1..], x `mod` 2 == 0]
liste_des_entiers_paires'' = [x | x <- [1..], even x]


-- On peut utiliser plusieurs variables se baladant dans différentes listes :
liste_de_produit = [x * y | x <- [1..], y <- [1..5]]

Une autre façon de définir une liste est d'utiliser la récusivité. Voici quelques exemples.

--"map f l" applique la fonction f sur chaque élément de la liste l
-- [a, b] est du sucre syntaxique pour a : b : [].
entiers = 1 : (map (1+) entiers)

Regardons ce qui se passe si l'on demande les trois premiers éléments de la liste, ce qui se fait avec "take 3 l". D'abord, on évalue "1 :" et connais donc le premier élément. Pour avoir le second, (map (1+) entiers). On applique donc map sur la liste, mais de façon paresseuse, c'est a dire qu'en ne calculant que l'application sur le premier terme. On obtient donc (1+)(1) = 2. puis, pour avoir le troisième élément, on doit appliquer (1+) au deuxième élément de la liste entier. Ça tombe bien, on vient de le calculer, c'est 2. On a donc pour troisième élément (1+)(2) = 3.

De cette façon, on aurais aussi pu définir la liste des entiers pairs, la liste des nombres de fibonacci (le hello world de la programmation fonctionnelle), ou la liste des nombres premiers (plus difficile).

Bon, c'est très beau tout ça, mais est-ce que ça sert vraiment (parce que, faire des listes infinies pour faire des listes infinies...)? Oui, ça sert, et voici un exemple simple et concret. Disons que vous participez au Google Code Jam. Vous devez fournir des réponse en respectant un certain format. Plus précisément, on vous donne une entrée de n éléments à traiter, par exemple n lignes contenant chacune un nombre, et vous devez fournir le résultat de votre traitement sous la forme "Case #i: <vos données>\n". En C++, on aurais itéré sur la liste de résultat (ou directement l'entrée) et provoqué l'écriture de "Case #i" sur la sortie standard juste avant celle de vos données. En haskell, on peut faire ça différemment :

boilerPlate :: [String]
boilerPlate = ["Case #" ++ show n ++ ": " | n <- [1..]]

standardOutput :: [String] -> [String]
-- zipWith f l1 l2 recole les deux listes l1 et l2 en utilisant la fonction f sur les éléments de chacune des deux listes.
-- La liste produite par zipWith fait la longueur de la plus courte.
-- Par exemple, zipWith (+) [1, 2, 3] [1, 1, 1, 1, 1] = [1+1, 2+1, 3+1]
standardOutput = zipWith (++) boilerPlate

-- Une fois votre sortie sous la forme d'une liste de String, il vous suffit de la donner à standardOutput pour obtenir le formatage attendu

On voit ici que la liste infinie boilerPlate contient tous les formatages possibles. Bien entendu, à chaque exécution, il n'y auras qu'un nombre finie d'entrées et de sorties, donc une partie finie de la liste qui sera utilisée.

En haskell, manipuler des listes ou des structures similaires est chose courante, et il y a un bon nombre de fonction dédiés. Par exemple map f l qui permet d'appliquer f sur les éléments de l, zip et zipWith qui permettent de souder deux liste en une unique (soit sous forme de liste de couple, soit en utilisant la fonction que vous fournissez). Mais ce n'est pas tout. Nous ne parlerons par exemple pas de foldr et foldl qui permettent a partir d'une liste d'éléments de l'écraser en un nouvel élément grâce à une fonction que vous fournissez (leurs usages est multiple. On peut implémenter facilement la somme/produit des éléments d'une liste, la conversion d'une liste de mot en une seul chaîne de caractère, la transformation d'une liste en un arbre binaire de recherche, etc).

Vous devriez avoir remarquer qu'en haskell, on aime bien concevoir de petites fonctions travaillant sur un élément de type a, et produisant un élément de type b, puis appliquer ces petites fonctions sur les éléments de structures de donnés plus ou moins complexe.

Cela a de nombreux avantages :

• Il est plus simple de concevoir une fonction de type Int->String qu'une fonction de type [Int] -> [(String, Int)], par exemple.
• On est plus générique ; Si l'on sais transformer du a en b, alors on sais transformer du [a] en [b], du Either a c en Either b c, et du Tree a en Tree b (où Tree a est un arbre binaire où chaque noeud contient un élément de type a).
• En cas de changement de structure mémoire, par exemple pour des raisons de performances, on minimise l'impacte sur le code à modifier. Si l'on souhaite passer de liste à des arbres, seul le traitement effectué sur les listes devras être ré-écrit pour les arbres, mais rien d'autre.

On se retrouve donc à se concentrer plus sur les types qu'on manipule que la façon dont on les manipule (qui est dictée par le type).

Cette affirmation n'est plus vrai quand on travaille dans des monades comme IO où le type n'indique pas beaucoup plus que "Il vas se passer quelque chose".

C'est à dire que l'on dispose d'un nombre important de façon élémentaires de transformer certaines données en d'autres, et les points cruciaux sont alors de:

• Bien choisir la façon dont seront représentés les données traitées
• Trouver les structures de données intermédiaires au cours du déroulement d'un algorithme.
• Résoudre le puzzle des types. Par exemple pour combiner un (a -> b) avec [[a]] pour produire un [b], il faut penser à ((.).(.)) (concat $) (fmap . fmap).

Si l'on sais exactement de quels donnés l'on part, et quels donnés on doit produire, il ne reste alors plus qu'à décrire les transformations nécessaire pour passer de l'une à l'autre. Par exemple, faire un programme de reconnaissance de caractère, c'est transformer une image en une chaîne de caractère. Pour peu que l'on parvienne à réduire l'écart entre les structures de donnés considérés (par exemple une image, puis une liste de rectangles de pixels représentant des lignes, puis une liste de liste de rectangles de pixels représentant des mots) il devient très simple de décrire la transformation (on a réussi a réduire le problème a savoir découper les lignes, découper les mots, découper les lettres puis reconnaître une lettre).

Si ce type de raisonnement appliqué au c++ conduit facilement à un code catastrophique, en haskell c'est très certainement l'une des routes les plus sur. Le système de types et de classes de type rendent cette approche encore plus efficace.

En C++ un type représente un ensemble de fonctionnalités. En haskell un type n'est rien d'autre qu'un ensemble possible de valeurs. On peut tout de fois préciser qu'un type peut être manipulé d'une certaine façon (ordonné, comparé, affiché...). On pourrait dire que deux éléments d'un type que l'on a construit peuvent être affiché, ou encore comparé, en le faisant instance d'une classe. Cela correspond a la surcharge de fonctions/opérateurs du C++ ; après avoir déclarer une structure struct St;, on peut surcharger l'opérateur de comparaison pour ce nouveau type par bool operator > (St &a, St &b);. Vient alors l'idée de ce que doit être quelque chose "d'affichable" ou de "comparable". C'est un type pour le quel on doit avoir certaines fonctions de définies. En java, il y à la notion d'interface, où l'on veut imposer l existence de certaines méthodes. Malheureusement, on ne peut le faire que lors de la déclaration d'un type, et l'implémentation de cette interface est faite "à l'intérieur" du type. En haskell, pas de fonctions membres, mais des fonctions tout cours. Ce qui fait que n'importe quel type pourra devenir instance de n'importe quel classe (terme haskell désignant une famille de type pour les quels on dispose d'un jeu de fonctions) et à l'instant où vous le désirerais. Le sens d'une classe en haskell est donc plus proche de celle de la théorie des ensembles (une collection d'objets [ici de types] qui respectent certaines conditions [ici, pouvoir être comparé, affiché...]) ou, si vous voulait vraiment une analogie en langage impératif, des interfaces du java. C'est donc très différent des classes C++.

Quand on prétend qu'un type est instance d'une classe, on doit fournir l'implémentation des fonctions de la classe, mais pas nécessairement toutes. Les classes fournissent souvent une implémentation des fonctions, souvent en terme récursif. Par exemple on pourrais définir a /= b à partir de == et a == b à partir de /=. De cette façon, il suffit de définir l'une des deux fonctions pour pouvoir immédiatement utiliser les deux opérateurs. (Le compilateur s'assurant que cela n'engendre pas de sur-coût en terme de performances.)

Voici par exemple la classe Eq, décrivant deux objets pouvant être comparé :

class  Eq a  where
class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool
    x == y = not (x /= y)
    x /= y = not (x == y)

On rend un type instance d'une classe de la façon suivante (exemple honteusement tirer de Learn You a Haskell) :

data TrafficLight = Red | Yellow | Green

instance Eq TrafficLight where
    Red == Red = True
    Green == Green = True
    Yellow == Yellow = True
    _ == _ = False

On définit l'égalité grâce au filtrage par motif, en définissant seulement l'opérateur ==.

Bon, à vrais dire, pour les classes comme Eq (comparable) et Show (affichable), on peut laisser haskell s'en charger comme un grand :

data TrafficLight = Red | Yellow | Green deriving (Show, Eq)

En fait, quand on parlera de foncteurs, foncteurs applicatifs ou monades, on parlera de type qui sont instances respectivement de Functor (Prelude.Functor), de Applicative (Control.Applicative) et de Monad (Control.Monad).

Les foncteurs (à nouveau, le terme est à prendre au sens de la théorie des catégories) constituent le point de départ vers les monades. Faisons un petit détour par les maths et définissons ce qu'est un foncteur (il n'est pas nécessaire de comprendre ce paragraphe pour la suite, c'est pour la culture).

La catégorie des types : Une catégorie 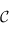est une collection d'ensembles. Ici, on regarderas la collection de tous les types hasell possible. Un ensemble seras donc un type. Ses éléments seront les valeurs qui sont de ce type. Par exemple Int seras un semble et 1, 4, 6 sont des éléments de cette ensemble. Il n'y a que deux éléments dans l'ensemble Bool, et une infinité d'éléments pour Integer. Pour que ce soit une catégorie, il faut qu'étant donné deux ensembles de notre collection 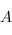et 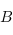, il existes une ensemble d'applications de 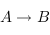. Dans notre cas ce seras toute les fonctions de type A -> B . On parle des "flèches de A vers B". Pour la culture, on note l'ensemble de ces applications .

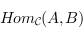Attention, pour que ce soit vraiment une catégorie, il faut quelques conditions sur ces flèches :

1) Si 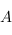est un élément de 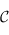, alors il faut que l'identité soit une flèche. Dans notre cas, on veut que la fonction id x = x de type A -> A soit bien une fonction haskell. Ce qui est le cas, puisque je viens de vous donner le code haskell qui permet de la définir :)

2) Si 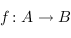et 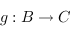sont deux flèches (respectivement de 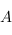dans 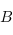et de 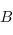dans 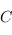), alors la composé 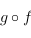est une flèche de 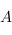dans 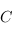. Dans le cas qui nous intéresse, cette règle est bien respectée car si f et g sont deux fonctions haskell, alors la composé est la fonction \x -> g (f x), que l'on peut aussi écrire f . g.

Donc, pour résumer : La collection de tous les types haskell est une catégorie. Si a et b sont deux types haskell, l'ensemble de toute les fonctions de a -> b sont appelés les flèches entre a et b.

Les foncteurs (covariants) : Un foncteur 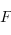d'une catégorie 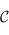vers une catégorie 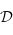est :

1) Pour chaque sembl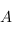e de 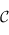, un ensemble de 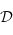qu'on noteras .

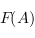2) Pour chaque flèche 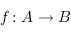entre des ensembles de 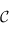, une flèche 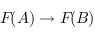qu'on noteras .

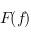3) Il faut que 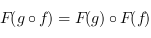et que 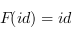. C'est à dire que composer des flèches avant transformation est la même chose que les composer après, et l'identité 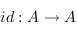(flèche qui ne fait rien) est bien envoyer sur l'identité .

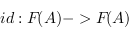Un foncteur est donc une façon de transformer une catégorie 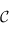en une partie (sous-catégorie) de .

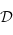Point culture (pour les curieux) : Les foncteurs contravariants sont simplement des foncteurs qui "renversent" les flèches, c'est à dire en transforment A -> B en F(A) <- F(B).

Ici, ce qui nous intéresse sont les foncteurs de 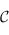dans 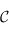(on dit des endofoncteurs). À partir de maintenant, on ne considère plus que la catégorie 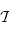des types haskell. Un foncteur Fonc, en haskell, est un foncteur de 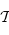dans 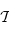. C'est à dire :

1) Une façon à tout type a d'associer un type Fonc a. Ainsi Fonc est un constructeur de type, par exemple Liste ou Arbre des exemples précédents. C'est peut-être le bon moment d'aller feuilleter quelques lien sur les constructeurs de type et leur "kind". Disons simplement qu'un type comme Int ou Bool est de kind "*" mais que Liste et Arbre sont de kind "* -> *". Cela signifie que ces deux dernier mangent un type T et fabrique des nouveaux types Liste T et Arbre T. Liste n'est donc pas un type, mais un constructeur de type.

2) Une façon à toute fonction f :: a -> b d'associer une fonction f' :: Fonc a -> Fonc b

3) Cette façon de faire doit transformer l'identité (\x -> x) :: a -> a en l'identité (\x -> x) :: Fonc a -> Fonc a

4) Cette façon de faire doit passer à la composition, c'est à dire que si l'on transforme f :: a -> b en f' :: Fonc a -> Fonc b et g :: b -> c en g' :: Fonc b -> Fonc c, alors g . f seras transformé en g' . f'.

Pour qu'un constructeur de type Fonc soit un foncteur, on le fait instance de la classe Functor définie comme suit :

class  Functor f  where
    fmap        :: (a -> b) -> f a -> f b

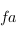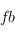Remarquez que l'on peut lire fmap :: (a -> b) -> (f a -> f b) ce qui signifie : fmap(fonctorial mapping) prend une fonction de type a -> b et la transforme en une fonction de type f a -> f b. On a donc bien une transformation d'une flèche de a vers b en une flèche de vers . Si l'on a donc un constructeur de type qui est instance de Functor, on a bien un endofoncteur de la catégorie des types. Maintenant que nous avons le sentiment que toutes nos considérations théoriques nous ont apporté une compréhension profonde du sujet, nous allons pouvoir les oublier et passer à la pratique.

A quoi sert un foncteur : Un constructeur de type fonctoriel, c'est un constructeur de type où l'on sauras mapper des fonctions. Si notre type Liste devient instance de Functor, et que l'on a un Liste Int, on peut construire rapidement une liste de tous ces nombres représenté par des chaînes de caractères. Il suffit de disposer d'une fonction Int -> String. Haskell nous en fournis une, c'est show. Alors, on n'a plus qu'a appliquer cette fonction sur chacun des éléments de la liste par map show liste.

Regardons comment rendre Liste instance de Functor :

instance  Functor Liste  where
    fmap f Vide = Vide
    fmap f (Element h t) = Element (f h) (fmap f t)
</paragraph>
<paragraph>
-- Maintenant, on peut mapper des fonctions sur des listes
estPositif n = (n >= 0)

listeEntiers = Cons 1 (Cons (-5) (Cons (-30) (Cons 4 Vide) ) )
listeEstPositif = fmap estPositif listeEntiers
-- listeEstPositif = Cons True (Cons False (Cons False (Cons True Vide)))

Si vous réfléchissez bien, ça ressemble beaucoup à ce que vous faites à chaque fois que vous appliquez un traitement aux éléments d'un container ; vous parcourez une liste, et vous appliquez votre procédure à chaque élément. L'avantage d'avoir une unique fonction fmap implémenté pour chaque type, c'est que si vous décidez de modifier votre container, vous n'aurez que très peut de changement à faire. Il suffira de rendre le nouveau container instance de Functor, alors qu'en C++, si vous utilisiez auparavant des containers de la STL, il vous faudra vous assurer que votre nouvelle structure fournie elle aussi des itérateurs, ce qui peut être assez lourd à fournir, voir impossible si vous n'êtes pas auteur de la classe.

Parmi les instances de Functor il y a donc les listes (les vrais listes []), mais aussi Maybe. On peut donc utiliser Maybe pour utiliser des valeurs dans un contexte. Par exemple :

divideBy :: Int -> Int -> Maybe Int
divideBy n m = if m == 0 then Nothing else (n `div` m)


doSomething :: Int -> Int
doSomething n = (n + 32) * 5


res = fmap doSomething (divideBy 3 7)

Il est très important de bien saisir le fonctionnement des foncteurs pour la suite. La dernière partie ne traitera que de leurs spécialisations : les foncteurs applicatifs et les monades.

Point culture : Et si l'on veux un foncteur contravariant en haskell? On peut prendre par exemple le constructeur de type "type Func a = a -> Int" et la fonction "map :: (a -> b) -> (b -> Int) -> (a -> Int) ; map f fa = fb . f". On construit bien une fonction de type "a -> Int" à partir d'une fonction de type "b -> Int". On a donc "inversé les flèches", puisque l'on part de "a -> b" pour obtenir du "Func b -> Func a".