Raytracer minimaliste en Haskell : Affichage d'une sphère

Bien, allons-y. Il nous faut une fonction capable de nous donner les couleurs à placer dans l'image. On veut donc une fonction getPixel :: Scene -> (Int, Int) -> [Word8] où le premier paramètre est « la scène », le second la position du pixel que l'on cherche à connaitre, et la valeur de retour est une liste contenant nos trois couleurs.

On ne sait pas trop pour le moment ce qu'est une scène, ni comment écrire la fonction. Mais ça ne nous posera pas de problème pour compiler le module. Ah, et tant qu'à faire, nous aurons besoin d'une caméra pour représenter la position depuis laquelle on regarde, et connaitre la taille de « l'écran » sur lequel viendront se dessiner les images.

module Raytracer (
  Scene,
  Camera,
  getPixel,
  ) where

import Data.Word

data Camera = Camera
data Scene = Scene
type PixelLocation = (Int, Int)

getPixel :: Scene -> PixelLocation -> [Word8]
getPixel = undefined

On doit inclure le module Data.Word pour utiliser le type Word8.

Remarquez que l'on a construit des types « vide » pour Camera et Scene. De même, appeler getPixel provoquerait une exception (si l'appel est vraiment exécuté). Mais on peut tout de même vérifier que nos types sont cohérents.

Pour que notre module soit compilé, il faut l'importer dans le module Main. Ajoutez donc la ligne suivante à la suite de toutes les importations.

import Raytracer

Appelons maintenant la fonction getPixel en modifiant la définition de tableData.

tableData width height = listArray ((0,0,0), (height, width, 3)) $ pixels
  where
    pixels = concat . map (getPixel emptyScene) $ [(x, y) | y <- [0..height - 1], x <- [0..width - 1]]

Nous avons besoin d'une scène vide, emptyScene, que l'on rajoutera dans le module Raytracer. Mais regardons déjà ces quelques lignes.

D'abord, pour plus de lisibilité, on va construire la liste de couleurs sous le nom pixelsList. On applique la fonction (getPixel emptyScene) qui est de type PixelLocation -> [Word8] sur chacune des coordonnées (x,y). L'ordre d'énumération est préservé, et c'est très important, car la première dimension du tableau est la hauteur, et ensuite la largeur. On veut donc que la liste contienne les pixels ligne par ligne. C'est pourquoi on énumère d'abord le y puis le x. Si quelques doutes persistent, reportez-vous aux listes en compréhension et aux listes comme monades.

En parlant de monades, cette histoire de "map-concat", ça ne vous rappelle rien ? C'est bien sûr l'opérateur >>= que l'on utilise sans le dire. Eh bien, disons-le !

    pixelsList = [(x, y) | y <- [0..height - 1], x <- [0..width - 1]] >>= getPixel emptyScene

Voilà qui est plus lisible. Comme promis, rajoutons une scène vide :

emptyScene :: Scene
emptyScene = undefined

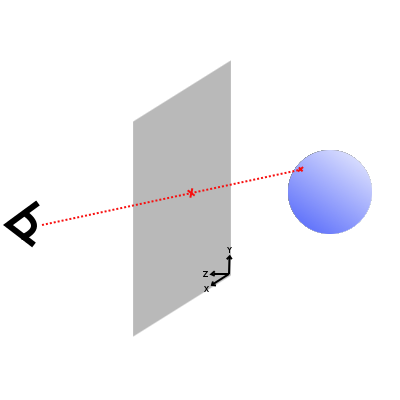
Pour raytracer des objets, il nous faut un point à partir duquel lancer des rayons. Ces rayons viendront intersecter les objets, et l'on saura alors à quelle distance ils se trouvent. On pourra aussi récupérer la couleur de l'objet, et l'angle entre l'objet et l'observateur, pour calculer la lumière. De plus, on ne projette pas des rayons n'importe où. On va construite un rectangle de la taille de l'image, découper ce rectangle en pixels, comme ceux de l'image que l'on veut générer, et projeter des rayons provenant de la position de l'observateur en direction de chacun de ces pixels.

De nombreux facteurs entrent en jeu. Où se trouve le plan par rapport à l'observateur ? À quelle distance ? Comment est-il orienté ? Comment le placer, gérer les changements de taille de l'image ?

Dans les jeux vidéo, ou plus généralement en 3D, on entend parler « d'angle de vision ». L'angle de vision est directement affecté par la distance entre le « plan de projection » (le plan dont on parle) et l'observateur (la position de la caméra).

On va décider que la caméra regardera toujours vers l'axe des Z négatif, et que le plan sera face à la caméra, parallèle au plan Z = 0. De cette façon, les x croissants seront sur la droite de l'observateur, et les y croissants vers le bas (comme notre image).

Et si l'on veut regarder dans une autre direction pensez-vous ? Eh bien, il suffira de faire tourner la caméra, chose qui sera identique à la rotation des objets raytracés. Mais n'allons pas trop vite en besogne.

De plus, une scène doit contenir des objets. Disons donc que nous avons une caméra, et une liste d'objets. Ne me demandez pas ce qu'est un objet :)

--Représentation des nombres réels
type RealRep = Double
--Représentation d'une position dans l'espace
type Location = (RealRep, RealRep, RealRep)
--Représentation d'une distance
type Distance = RealRep
--Dimensions du plan
type PlanWidth = Int
type PlanHeight = Int
type PlanSize = (PlanWidth, PlanHeight)

--Représentation de l'observateur
data Camera = Camera Location Distance PlanSize

--On object raytracable
data Object = Object

--Une scène
data Scene = Scene Camera [Object]

--Une coordonnée dans l'image
type PixelLocation = (Int, Int)

--Une fonction qui fournit une camera centrée en 0,0,0
buildDefaultCamera :: Distance -> PlanWidth -> PlanHeight -> Camera
buildDefaultCamera distance planWidth planHeight = Camera (0,0,0) distance (planWidth, planHeight)

On en profite pour ajouter une méthode permettant de construire une caméra par défaut. N'oublions pas de revoir les exports :

module Raytracer (
  Scene,
  Camera,
  Object,
  getPixel,
  emptyScene,
  buildDefaultCamera,
  ) where

Il nous faut maintenant construire un vecteur provenant de la caméra, à partir d'une scène et des coordonnées d'un pixel. De plus, il faut que le vecteur soit de norme 1, de façon à ce que la distance soit simplement le nombre de fois où il faut placer des copies de ce vecteur bout à bout pour atteindre l'objet.

En fait, il suffit que tous les vecteurs aient la même norme, car on ne cherchera qu'à comparer les distances entre elles. Si tous les vecteurs n'ont pas la même norme, c'est dû au fait que la distance du point d'observation aux angles du plan est plus grande que la distance d'observation au centre du plan (la distance indiquée dans la caméra).

Commençons par le nécessaire pour construire un vecteur à partir des coordonnées d'un pixel, et une fonction pour rendre un vecteur unitaire.

Au passage, on crée un nouveau module Tools, et l'on déplace quelques types « élémentaires ». N'oubliez pas d'importer notre nouveau module dans le module Raytracer.

module Tools (
  Location,
  Distance,
  RealRep,
  Vector,
  Ray,
  normalise,
  int2RealRep,
  ) where

--Représentation des nombres réels
type RealRep = Double

--Représentation d'une position dans l'espace
type Location = (RealRep, RealRep, RealRep)
--Représentation d'une distance
type Distance = RealRep

--Un vecteur
type Vector = (RealRep, RealRep, RealRep)
type Ray = Vector


normalise :: Vector -> Vector
normalise vector@(a, b, c) = (a / n, b / n, c / n)
  where
    n = norm vector

norm :: Vector -> RealRep
norm (a, b, c) = sqrt(a^2 + b^2 + c^2)

int2RealRep :: Int -> RealRep
int2RealRep = fromIntegral

On aura aussi besoin de convertir des entiers en RealRep dans quelques instants, alors tant qu'à faire, on définit un alias pour fromIntegral, qui s'occupera des conversions de types numériques.

Implémentons une fonction computeRay :: PixelLocation -> Scene -> Vector. Pourquoi la scène en dernier argument ? Parce que tout ce que l'on va produire va dépendre de la scène, et l'on peut donc considérer tous les résultats comme « valeur dans un contexte ». Humm, vous avez dit monade ?

--Construit un rayon à partir d'un pixel
computeRay :: PixelLocation -> Scene -> Ray
computeRay (x, y) (Scene camera objects) = normalise (vx, vy, vz)
  where Camera _ distance (planWidth, planHeight) = camera
        halfPlanWidth = planWidth `div` 2
        halfPlanHeight = planHeight `div` 2
        vx = int2RealRep (x - halfPlanWidth)
        vy = int2RealRep (y - halfPlanHeight)
        vz = -distance

On commence par diviser la largeur et la hauteur par deux, pour « centrer » le plan sur l'axe des Z. On calcule alors un vecteur de coordonnées (vx, vy, vz), qui relie le point (0, 0, distance) au plan Z = 0. On regarde donc la différence entre les coordonnées (0, 0, distance) et le point (x - halfPlanWidth, y - halfPlanHeight, 0) du plan Z = 0. La position de la caméra n'a aucune importance dans ce calcul, car quelle que soit la translation que l'on applique a la caméra, les vecteurs (les directions dans lesquelles on regarde) ne sont pas changés. La position de la caméra entrera en jeu plus tard, comme « point de départ » du rayon.